Hyperbolic Tilings

I have always been fascinated by the Escher tilings like Circle Limit III below:

I wanted to understand how to generate similar tilings. One category of tilings is generated by a triangle group : reflections through the edges of a triangle:

But those triangles look curved ? Indeed, they are triangles in the Poincaré representation of the Hyperbolic plane.

What’s interesting is that there is an infinity of triangle groups. The hyperbolic plane has a richer set of symmetries than our standard Euclidean plane.

But it is not very easy to work in the Poincaré representation. There is an another way to look at it by borrowing some ideas from the Minkowski space of Einstein relativity.

For generating those pictures I am working in $\mathbb{R}^3$ but using a different metric than the Euclidean one:

\[x^2+x^2-z^2\]

The Hyperbolic plane is then related to the pseudo-sphere. A sphere of radius $-1$ but where the radius is computed with above metric.

Then, I am looking at triangles on this pseudo-sphere. By analogy with a normal sphere, a triangle edge is the intersection with a plane containing the two vertices of the edge and passing through the origin.

Computing the reflection through this plane is easy once you know the vector orthogonal to the plane.

In Euclidean space, computing this vector would be easy with the cross-product since we already have two vectors in the plane : from the origin to the 2 vertices of the triangle edge.

We can create a similar cross product for the new metric we are using.

We can combine the metric tensor and the Levi-Civita symbol in 3 dimensions to create a gadget which is consuming 2 vectors and generating a vector in an antisymmetric way.

Using this gadget we can easily compute reflections through the edges of our triangle.

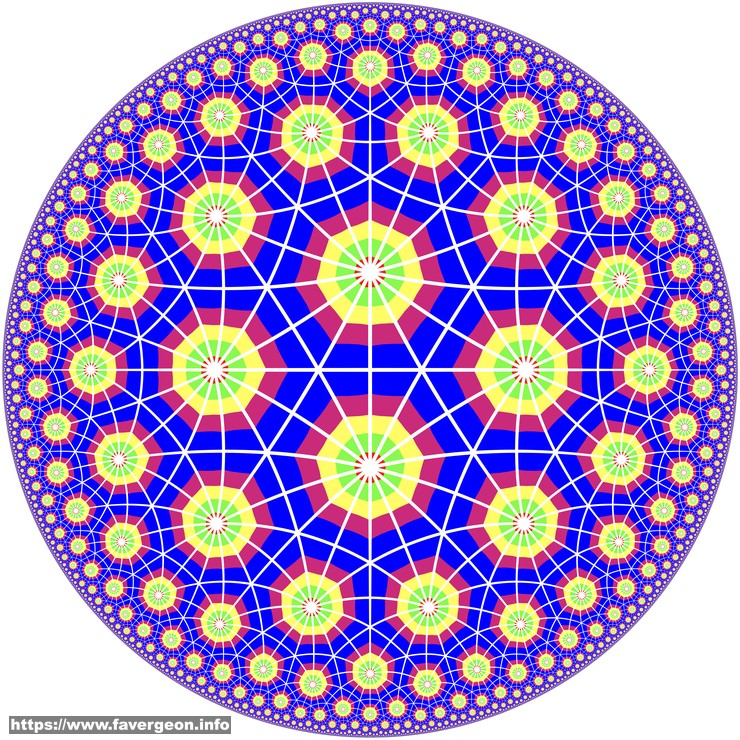
Now starting from a point in the Poincaré model, we map it back to our 3D space and compute its images through the triangle reflections until the image is back into the original triangle. Then we map it back to the Poincaré model and look at the color of this point in the original triangle.

If the original triangle is containing a colored pattern, then we obtain a tiling that no more look as something generated with triangles:

Then we can generalize and use a video instead of a pattern:

We can also apply rotations and translations to the Hyperbolic plane. In the Poincaré representation, it is done through Möbius transforms of the complex plane:

It is also possible, using analytical transforms, to map the disk to other geometrical shapes and without distorting the angles. For instance, we can get a model that is a strip: