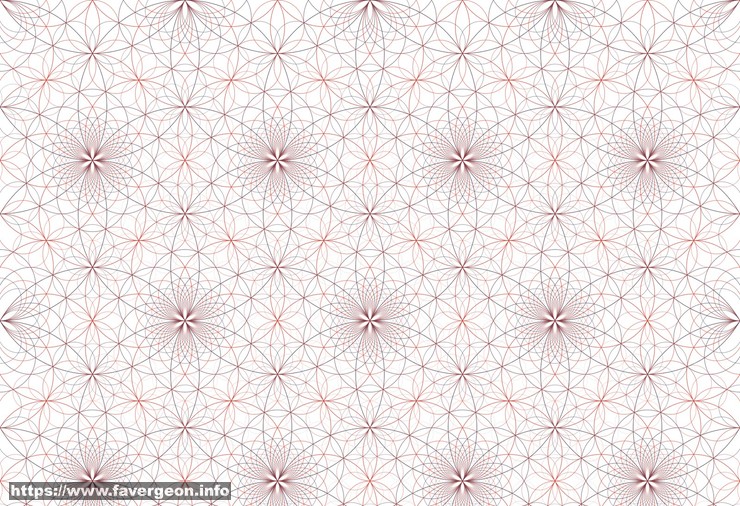
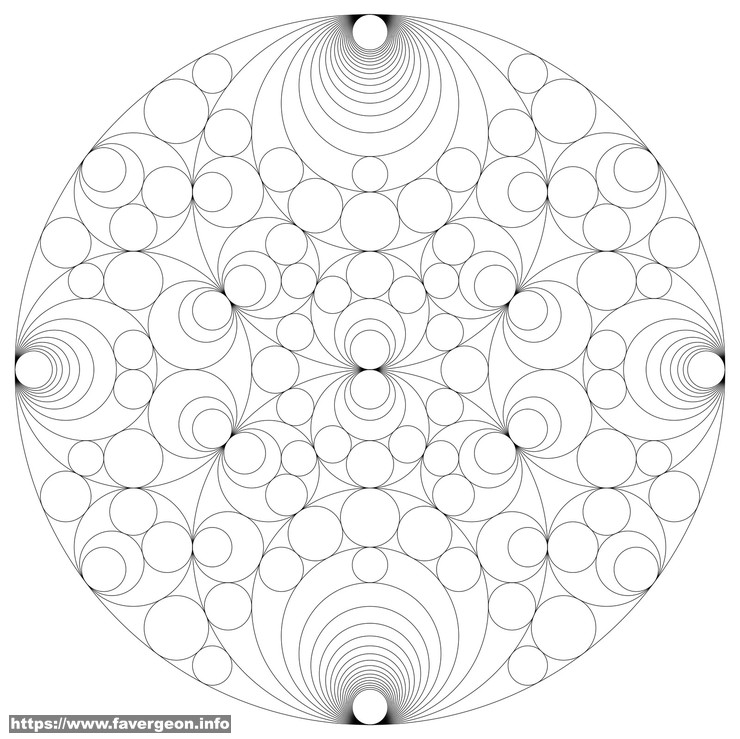
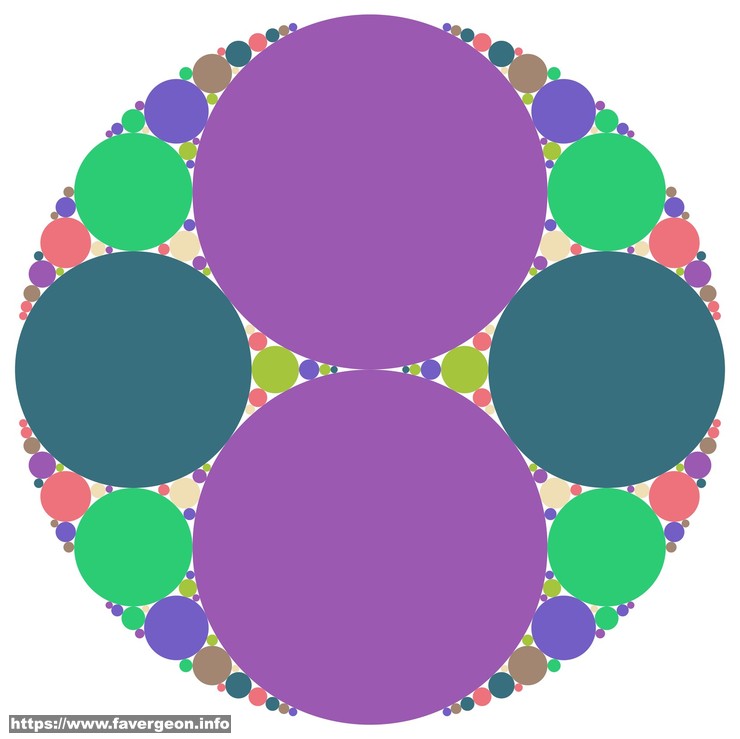
Schmidt Arrangements
The beautiful picture above is a Schmidt Arrangement : the orbit of $\mathbb{R}$ under a specific group of Mobius transformations.
The Mobius transformation of a complex number $z$ is
\[f(z)=\frac{az+b}{cz+d}\]If the coefficients $a,b,c$ and $d$ are restricted to the integers of a complex quadratic field then we get a Schmidt Arrangement.
The integers $O_k$ of a complex quadratic field $\mathbb{Q}(\sqrt D)$ are of the form:
\[a + b \sqrt D\]if $D-1$ is a multiple of $4$ and otherwise:
\[\frac{a}{2} + \frac{b}{2} \sqrt D\]with $a$ and $b$ being integers and odd in the later case.
You can find more about Schmidt Arrangement in the following pages:
- https://math.katestange.net/illustration/
- http://math.colorado.edu/~dama4729/
- https://blogs.ams.org/visualinsight/2015/03/01/schmidt-arrangement/
On above links, there is a Sage notebook that I have recoded with Mathematica. So all bugs are mine.
I have contacted the authors (Kate Stange and Daniel E. Martin) to understand a bit more how the algorithm is working. Here is my understanding (mistakes are mine and not from the authors of the original algorithm).
To each circle of a Schmidt Arrangement, you can associate a center $c$, curvature $b$, and co-curvature $b’$ (curvature of the circle you get with an inversion).
The curvature $b$ and co-curvature $b’$ are multiple of $\sqrt{|D|}$ (So, in the API of the functions, we use the integer factor to express the curvatures).
The center $c$ of the circles are in $i O_k$.
A circle is part of the Schmidt Arrangement if :
\[b b' = c \bar c - 1\]Said differently, if $\frac{c \bar c - 1}{b}$ is a multiple of $\sqrt{|D|}$.
The algorithm is iterating on curvature (up to a max) and on position (between some bounds) and checking if the above divisibility condition is true. If it is, the circle is part of the arrangement.
But, if you look at the details in the Sage notebook, you’ll see that the algorithm is in fact using $2$ different parameters $s$ and $t$ and from those parameters the positions are computed. I have not yet understood what are those parameters.
Also, when I am talking about circles or lines, I am in fact talking about an extended concept on the Riemann sphere. A circle can be degenerate and be a line in the plane. The algorithm is managing this case but I have not tested this part and I am not using the line parameter which can be found in the original Sage notebook.
The goal is to make beautiful pictures and I did not want to spend too much time on the details and the theory.